Quantitative Analysis
For more information, please read about my other professional skills

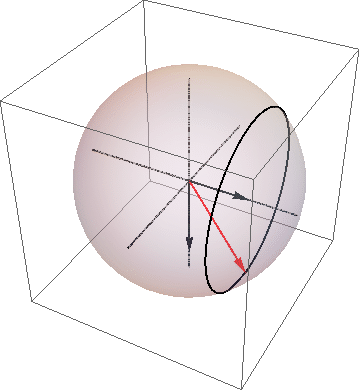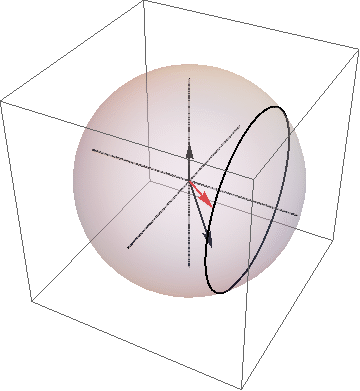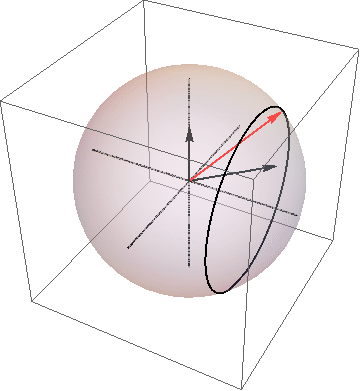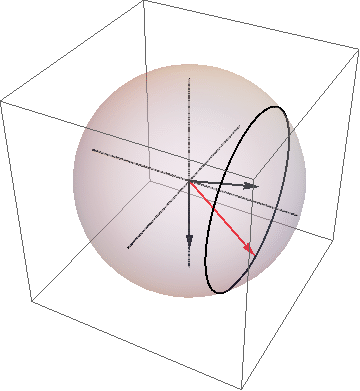
Differential equations are one of the most important mathematical tools in theoretical physics. In my research, I used differential equations to understand the time evolution of a qubit state. The normal evolution of qubits involves a simple solution to the Schrodinger Equation. When there is a driving force that is resonate with the energy spacing of the two states of a qubit, then the solution of the Shrodinger Equation is a bit more complex, but still uses the standard techniques of calculus. The measurement of solid-state qubits involves forces coming from stochastic noise that requires the techniques of Ito calculus. Each stage of evolution must be analyzed separately using the appropriate techniques.

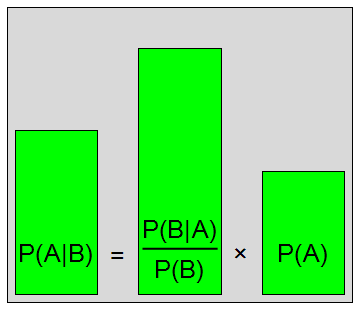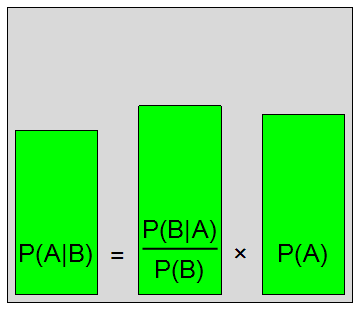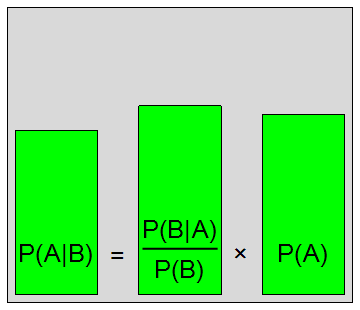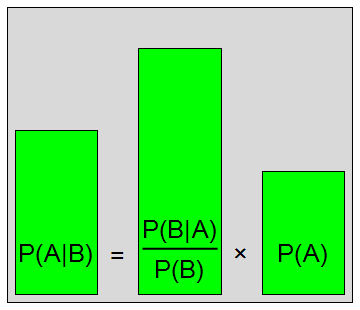
Bayesian Analysis

Bayes' Theorem is a very famous and fundamental theorem in probability theory. Simply put, it describes quantitatively how to adjust one's beliefs when new evidence is considered. For instance, it is more likely that a person with long hair is a woman because it is more likely that women have long hair in our culture. In simple logic, if A implies B, then one cannot assume that B implies A. It is important to remember that conditional probabilities are statistical correlations, which are expressed in similar terms to logic; however, these cannot be interchanged when making logical arguments. Implying, correlating, and causing are extremely different verbs; remember, correlation does not imply causation.

Combinatorics

Combinatorics is an especially elegant system for counting possibilities. I used combinatorics as a tool to calculate the frustrated magnetic ground state of electrons on a Kagome lattice. Very simply, a complete basis for the state space of N electrons can be found by counting all pairwise connections of N points spread evenly around a circle (shown to the left).